Some map stuff

I’ve been playing around with map projection and GIS tools for a while now, ever since I got addicted to the MapPorn subreddit and seeing some good-looking high resolution maps.

Reprojecting a Mercator map into an Equirectangular one

I got a bit bored after reprojecting an equirectangular map into something else too many times, but unfortunately the projection tools I used don’t support reprojecting from any other projections, so I decided to look up for methods to reproject other projections. I found out that QGIS is capable of doing so for free, so I went ahead and downloaded it.

However, a problem I immediately noticed is that the input file needs to have a georeferencing file accompanying it, otherwise it will always fail to reproject it. Well too bad. Because I literally don’t know how to georeference these maps I just stopped working on it for a while. It wasn’t until I found Flex Projector that I was finally able to do this easily, as the tool has a built-in automated georeferencing functionality. The tool itself isn’t very stable and tends to fail in projecting certain types of maps (more on that later), but at least it worked.

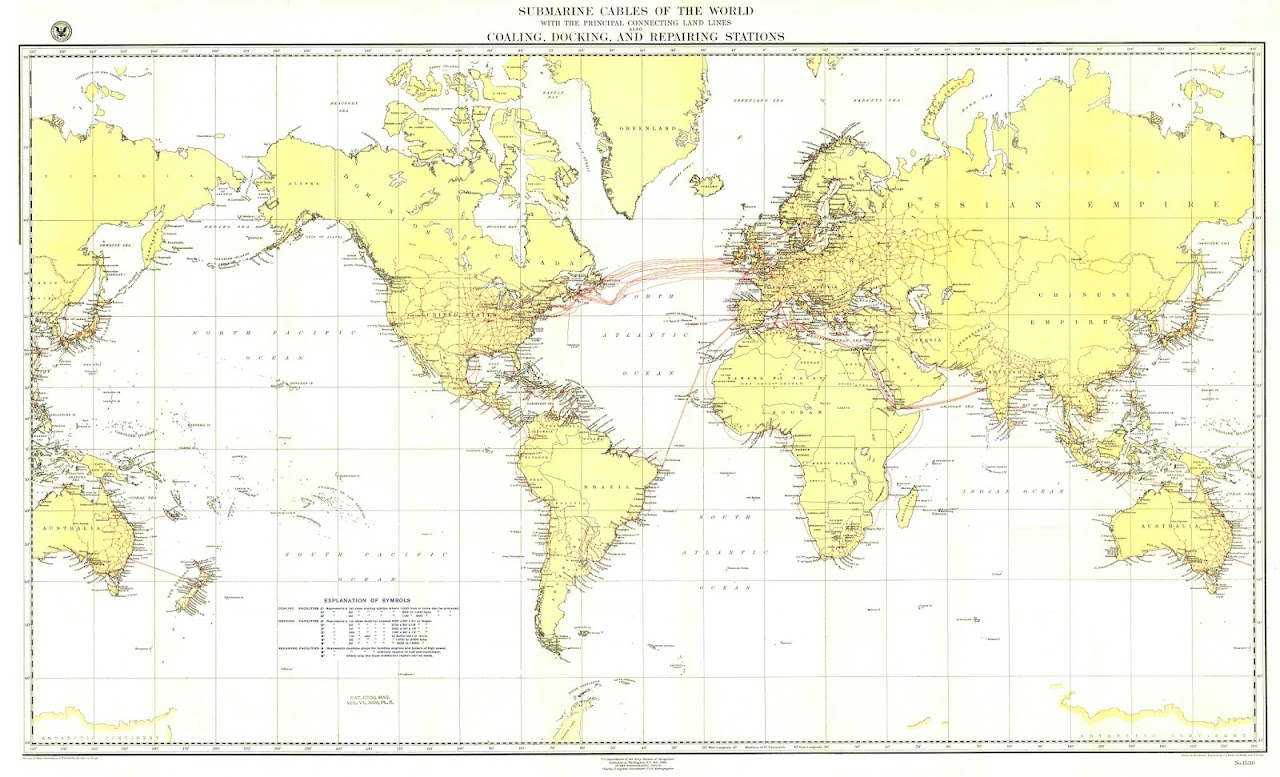
I started out by looking for a usable Mercator map to reproject. For this one I picked this vintage 1896 Nat Geo map of world submarine cables because I like how old it is and reprojecting these kinds of old maps can be a bit cool. This was before the Van der Grinten projection even existed, so it makes sense they picked this projection to display this map, and I think this is the only Nat Geo world map I have in my collection to use Mercator.

There were some problems I noticed with this map however. It’s not centered on the Prime Meridian and the map’s longitude ends at 160 E instead of 180 E, and the left and right portions of the map loops. I also noticed that the map is slightly tilted (lines drawn over the meridian lines with an image editor don’t line up), so I went ahead and did some adjustments in Photoshop, such as rotating the image ever so slightly so that the drawn lines can line up acceptably, copy-pasting the 160 E to 180 E regions from the left side of the map and pasting it to the right, cropped that looping regions on the left, and finally cropping the whole image so that only the map’s content remains.

Next, I fired up Flex Projector and exported an equirectangular silhouette map with the Mercator projection using the same width as our submarine cable map to prepare the georeferencing data for use in QGIS, as well as to align the source map to match the georeferencing data’s expectations. This map crops the poles pretty early, so those alignments are required to make this work, which leaves some empty spaces that are needed for QGIS to reproject it properly.

To do this I opened up the silhouette map in Photoshop, pasted the source map over it, and try to line it up as good as possible. Now because this is a hand drawn map, some inconsistencies with the silhouette map will be present, so to place things more accurately I exported a Mercator outline map with 10-degree graticules using Flex Projector again, and line it up with the silhouette map. It helps that our source map has graticules spaced every 20 degrees (Flex Projector only supports 10 degree graticules though), so I tried to align it with the source map’s graticules as well.

The silhouette map used to line up the source map	Aligning the source map with Photoshop
Oh hey, those cropped portions of Greenland line up quite nicely with the outline map!	Final result. Note the empty spaces at the top and the bottom of the image.

I then loaded the map in QGIS to reproject it, using EPSG 3785 (Popular Visualisation CRS/Mercator) as the source CRS and EPSG 4326 (WGS 84) for the target CRS. This outputs our submarine map to an equirectangular projection and voila, we’ve successfully converted this Mercator map into an equirectangular one.

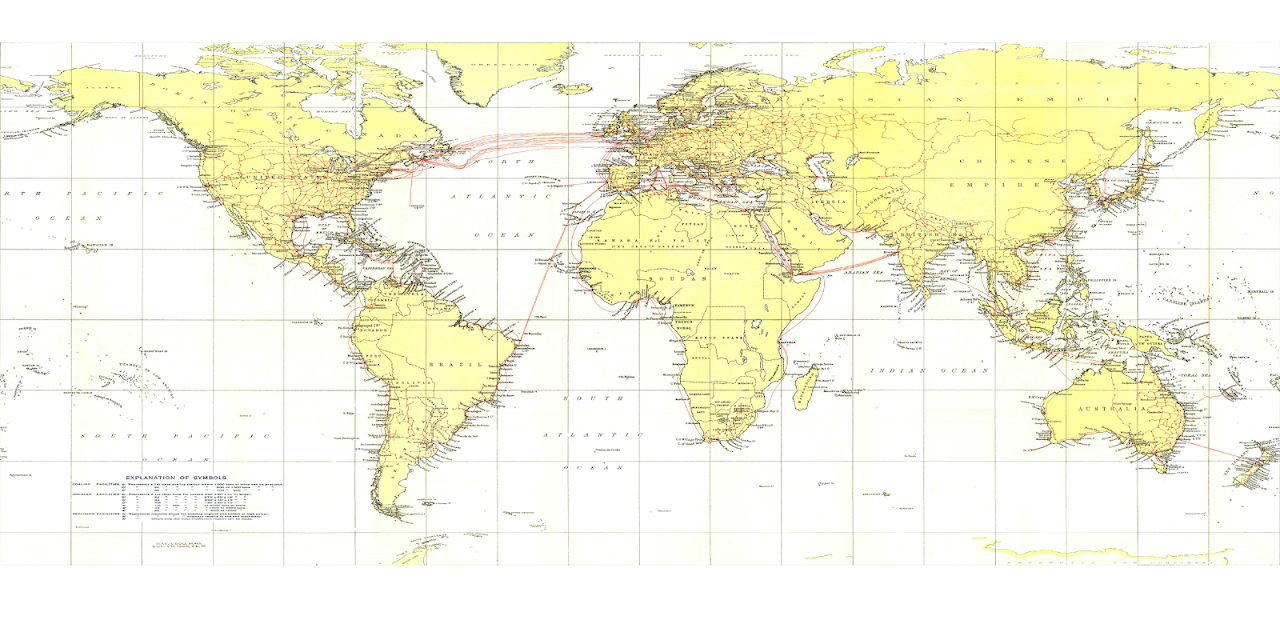
Click the image to view it in its full resolution

One thing I noticed is that because Mercator can’t show the entire world and Flex Projector outputs the map that’s cropped at 85 N/S, the aspect ratio for the map isn’t 2:1. Also, the output file’s resolution is way bigger than the input, so to fix this I resized it back to a smaller image with a width of 4256 pixels, and fixed the aspect ratio to 2:1, which leaves even more empty spaces, but again, necessary for further reprojections. The above image is actually the one with these adjustments already added.

Interrupting pseudocylindrical maps

It turns out that most, if not all, pseudocylindrical and similar types of maps can be interrupted. NASA’s G-Projector software supports interruptions of some pseudocylindrical projections (Goode homolosine, Mollweide, Sinusoidal) but unfortunately doesn’t offer it for most other pseudocylindrical projections. For example, the McBryde P3, which is based on Craster parabolic projection can be interrupted (and is in interrupted format by default), but the original parabolic projection itself can’t.

I looked up for a way to interrupt these projections myself and found this answer on Stack Exchange. It basically requires an image editing tool (I used Photoshop) and a bit of patience. I’ll just put it here for convenience:

If you look at a random example of the interrupted sinusoidal, each perfectly vertical meridian corresponds to a single sinusoidal projection.

For that example, you’re looking at sinusoidals centered on longitudes: -160,-100,-60, …

Then, cut and shift the parts to line up: The bottom left part is composed of longitudes -180..-100 and latitudes 0..-90, and projected with a center longitude of -160. The next part is longitudes -180..-40 and latitudes 0..90, projected w/ a center of -100. And so on (the example I linked was pretty intricate & there might be funny business going on in Russia; it doesn’t look like a vanilla sinusoidal there).

It doesn’t have to be sinusoidal; any pseudocylindrical, lenticular and other similar projections can be used, such as the Robinson or Hammer projection. However, it’s best to use a projection that has a straight equatorial line to make it easier to cut the north and south parts. The projection also doesn’t need to be equal area; while most of the commonly used interrupted projections are equal area (e.g. Goode homolosine), compromise projections (e.g. Winkel tripel) can still be used, resulting in an even more minimum-error map.

Here are some examples.

Equal Earth

The Equal Earth projection is a new pseudocylindrical equal-area projection designed by Tom Patterson in 2018, and was inspired by the Eckert IV and Robinson projections. It was made in response to the adoption of the Gall-Peters map by Boston public schools.

This example uses the Goode interruption pattern (displayed as “Interrupted: Continents” in G.Projector), but any interruptions can be used.

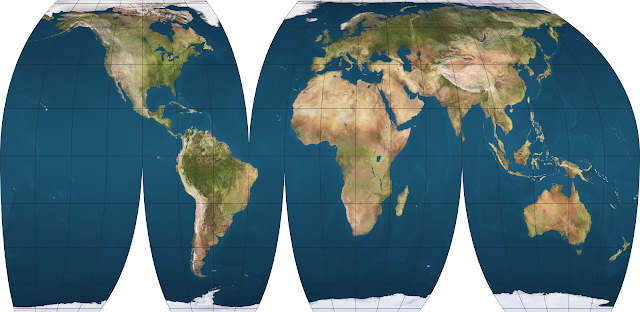
Interrupting this map reveals a substantial vertical stretching on low- and mid-latitude regions.

Fahey

The Fahey projection is a modification of the cylindrical stereographic projection designed by Lawrence Fahey in 1975. The parallels are spaced for a Gall stereographic based on a cylinder secant at about 35° instead of 45°, making it closer to the less-known BSAM cylindrical, which uses a standard parallel of 30°.

This example uses the Baker interruption pattern, which is used for the Baker dinomic projection.

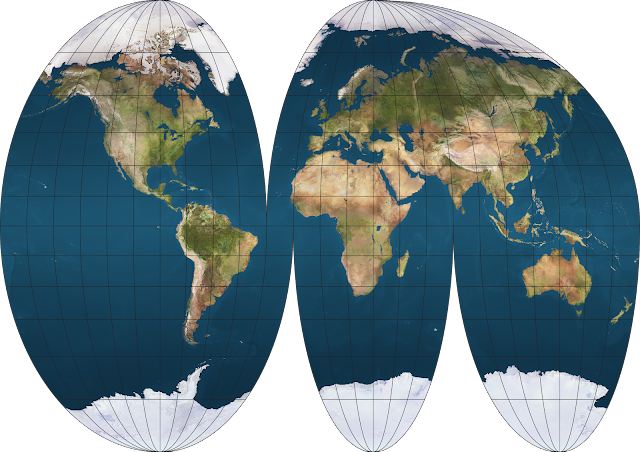
Ortelius oval

I know that literally no one uses this very old projection, but this one is interesting because although it appears to be a pseudocylindrical projection, it doesn’t qualify as one because the meridians are not equally spaced along the parallels, so it doesn’t belong to any common types of projection. If I had to name what kind of projection this is, I’d say it’s a “pseudopseudocylindrical projection”.

This actually looks pretty neat for an obsolete projection.

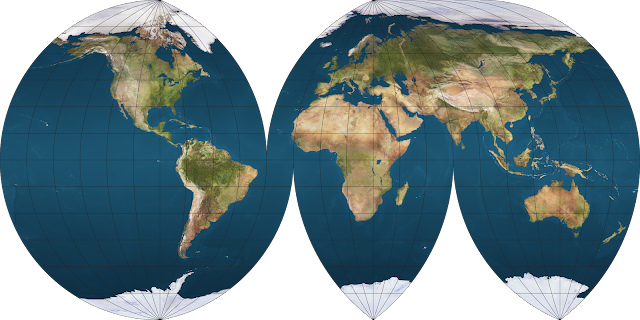
Winkel tripel

Here’s something you might have been waiting for: the Winkel tripel projection, now in interrupted form. If you like Nat Geo’s preferred compromise projection, you better see this.

Looks nice.

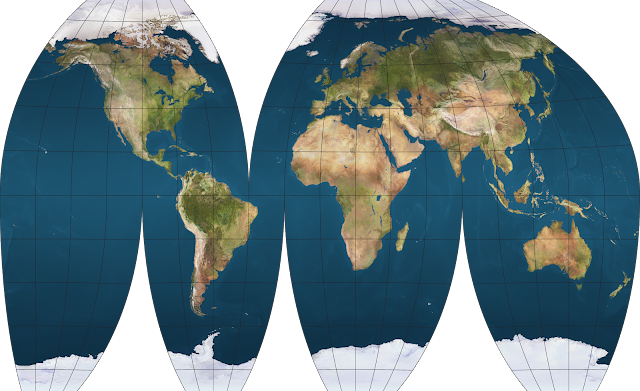
Robinson

Another excellent minimum-error projection in interrupted form. To be honest it looks better than the interrupted Winkel tripel.

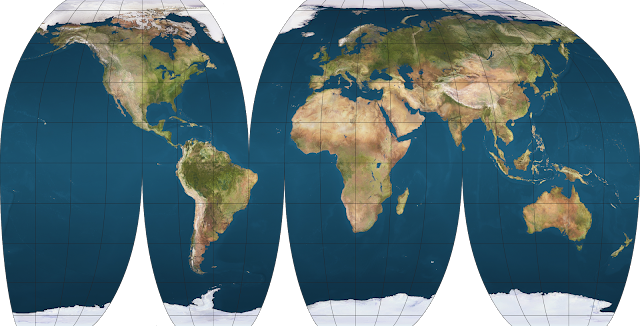
I prefer Robinson because it's got less vertical stretching on the low- and mid-latitude regions