New pseudoazimuthal projections
It turns out it’s actually quite easy to make pseudoazimuthal projections without the knowledge of making the equations for it. They are made by halving the longitudes, projecting it to an azimuthal projection, and stretching the result into a 2:1 ellipse. Using an image editor and map projection software, one can do the following to get the same results:
- Using an image editor, compress an equirectangular world map into a 1:1 square, and then edit the canvas size so that the width is twice the height of it again. This is done to avoid the projection software from correcting the map’s aspect ratio.
- Project the equirectangular map with an azimuthal projection and limit the projection range to a hemisphere. This is not possible with gnomonic or vertical perspective projections, meaning that they won’t show the entire world.
- Stretch the result so the width becomes twice the height of the image again, and you’re done.
The only drawbacks of using this method are you won’t get to know the equations, everything has to be done manually, and you can’t get a visualization for the distortion patterns of the projections.
Airy pseudoazimuthal
The Airy projection is a minimum-error azimuthal projection designed to minimize areal and angular distortions.
Quoting from Snyder’s “Flattening the Earth” book:
[Airy] approached the development of his projection with a goal of having a minimum “total evil” determined by what he called “Balance of Errors”. His “Projection by Balance of Errors” is neither perspective, conformal, nor equal-area, but it is a compromise appearing very much like the azimuthal equidistant projection, especially if limited to about one hemisphere. Airy’s specific approach was to minimize the sum of the squares of the erors in scale both along and perpendicular to the radii from the center of projection. For the polar aspect, these measurements are along meridians and parallels, respectively.
I’m not really sure if the pseudoazimuthal version is also good enough in minimizing distortions, but it’s definitely a compromise projection.

Breusing geometric pseudoazimuthal
The Breusing geometric projection is another minimum-error azimuthal projection. It balances the shape distortion of the azimuthal equal-area projection and the area distortion of the conformal stereographic projection by using for a given point a radius from the projection center equal to the geometric mean of the radii as calculated for these two projections.

Breusing harmonic pseudoazimuthal
The Breusing harmonic projection is a modification of the Breusing geometric, named so because it uses the harmonic mean of the same base projections as those used by Breusing for his geometric mean, namely, the stereographic and the Lambert azimuthal equal-area projections. In appearance, it strongly resembles the Airy projection.

Gott-Mugnolo pseudoazimuthal
The Gott-Mugnolo azimuthal projection was designed to minimize distance errors. It is based on the azimuthal equal area projection, so the end result looks rather similar to the Hammer projection, but is a compromise projection.

Pseudognomonic
The gnomonic projection can only show less than a hemisphere, and forcing it to go very close to it will cause severe distortions. It’s still possible to create a local or regional map with this though.

The pseudognomonic projection showing a half of the world. Distortions are still acceptable at this scale.

The pseudognomonic projection showing two-thirds of the world. Distortions start to become noticeable at this scale.

The pseudognomonic projection showing 17/18th (around 94.4%) of the world. At this point, the distortions are so extreme that the map is practically useless and ridiculous.
Pseudorthographic
This was developed by Daniel Strebe (developer of Geocart) in 2016, so you might find the equations there. I made this thing manually though since Geocart is expensive as hell.
It’s able to show the entire world because an orthographic projection projects the earth from an infinite distance, which means it’s able to show a whole hemisphere, which is exactly what’s needed to create the pseudoazimuthal projection.
The projection looks pretty awful though, so I don’t see any reasons for anyone to use this. Landmasses near the center of the map are significantly inflated, while those on the edge of the map are shrunk down and barely noticeable. It also loses the common purpose of having an orthographic map in the first place: to simulate a globe.

Pseudostereographic
This was developed by Justin Kunimune in 2017 and is available in his Map Designer software. He described it as “the next logical step after Aitoff and Hammer”. Despite being based on the stereographic projection, which is conformal, the resulting map isn’t. However, the angular deformations are somewhat more controlled here at the cost of having a much higher areal distortion than Aitoff or Hammer.
Because this projection exists in the Map Analyzer/Designer software he made, the distortion patterns can be visualized with it.

This one was made using Map Designer instead of by hand.


Distortion comparison of the pseudostereographic (left) and Aitoff (right) projections.
Wiechel ellipse
The Wiechel pseudoazimuthal projection is a modification of the azimuthal equal-area projection in an attempt to make it both equal-area and equidistant. It essentially looks like a pinwheel and has some severe angular deformations because of it. Turning this into a Hammer-like map may probably still retain its area equivalence, at the cost of losing its equidistant properties and terrible angular deformations, so it’s more of a novelty.
I don’t wanna say “Wiechel pseudoazimuthal” for this modified version because the original one is already a pseudoazimuthal projection.

Bonus: Logarithmic pseudoazimuthal
The logarithmic azimuthal is based on the azimuthal equidistant projection, designed to magnify the central portion of the map. It can also be used humorously by blowing up the central portion excessively.
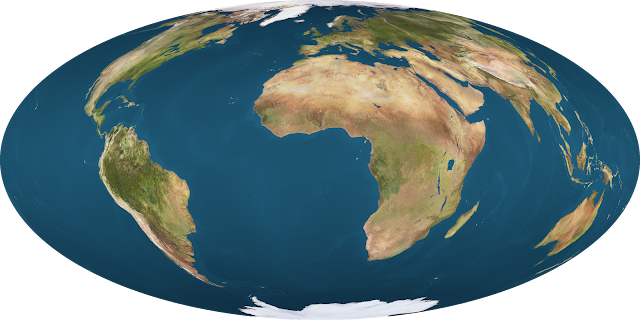
The logarithmic pseudoazimuthal projection with a cental scaling of 5.

Who says you can't have fun with map projections?