I’m a dead bored person. Because of that I sometimes do pointless stuff just for my entertainment. This time though it’s about me messing around with map projections. Equirectangular/plate caree projection to be exact. I take some world maps from some sources, and mess around with it.

Why equirectangular?

Equirectangular is used because it’s easy to use on map projection tools, not to mention that most of them only supports that as the input file. Other projections would require some tedious fiddling that takes too much time (e.g. Mercator, Winkel tripel, Robinson).

What I did to make these maps able to be projected properly

Most of the maps I took are simply difficult to project because they either have some weird extra parts in it or the proportion is off. To compensate for this, I used Photoshop and overlaid a proper map image on it and scaled it accordingly until it fits well enough.

Randall’s “equirectangular map” from his xkcd #977 comic

The “map”

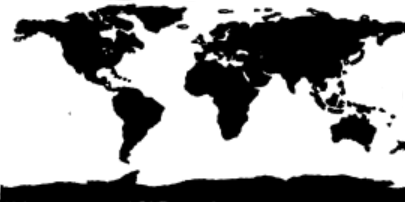
I did some adjustments to make it usable for projection

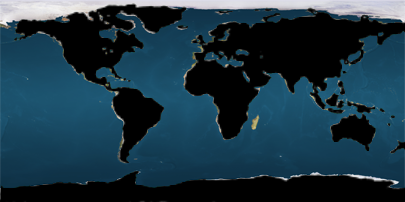
It turns out it fits pretty well on an actual equirectangular map! Sadly he didn’t include Madagascar though, at least on this particular projection…

Hey, it fits well with Dymaxion!

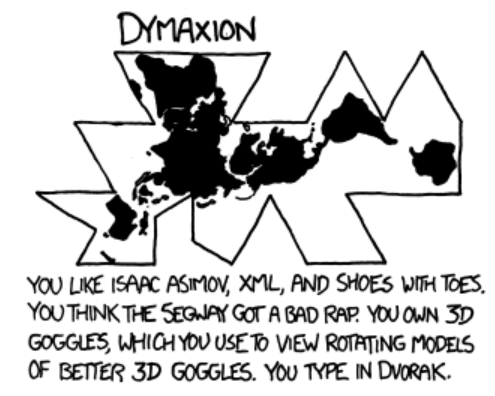
Now lets compare it with his hand-drawn version of Dymaxion projection. Notice the presence of Madagascar on this one.

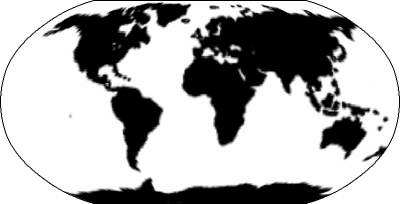
Robinson projection applied on it. My personal favorite besides the Winkel tripel.

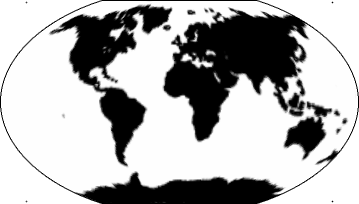
Winkel tripel projection.

AuthaGraph (clone) projection.

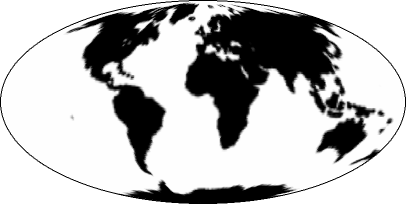
Mollweide projection. A thing that disturbs me the most with this comic is that he didn’t include Mollweide, Hammer and Behrmann projections despite them being quite popular and the comic including Hobo-Dyer, Gall-Peters and the more obscure Goode homolosine projections, all of which are equal-area projections.

Hammer projection.

Orthographic projection. Contrary to what he said, globe-like projections do exist, and they are the orthographic and general perpective projections.

When compared, it appears that this one is an orthographic projection.